Через точку на основании равнобедренного треугольника провели два отрезка, параллельных
боковым сторонам треугольника. Найдите периметр образовавшегося параллелограмма, если боковая сторона треугольника равна 6.
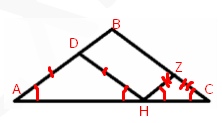
Решение
\( ∡A=∡C \) – по условию, т.к треугольник – р/б
Нам даже дали, что четырехугольник параллелограмм, т.е облегчили задачу, т.к пришлось бы еще это доказывать, хотя делается это легко
\( AB∥HZ \) , значит \( ∡A=∡ZHC \)
\( DH∥BC \), значит \( ∡DHA=∡C \)
И получилось, что треугольники \( ADH \) и \( HZC \) – р/б, а значит
\( DH=AD \) и \( HZ=ZC \)
\( P_{паралл}=DH+DB+BZ+HZ=AB+BC=12 \)
Ответ: 12
