Концы отрезка АВ лежат по разные стороны от прямой . Расстояние от точки А до
прямой l равно 23, а расстояние от точки В до прямой l равно 45. Найдите
расстояние от середины отрезка АВ до прямой l .
Решение
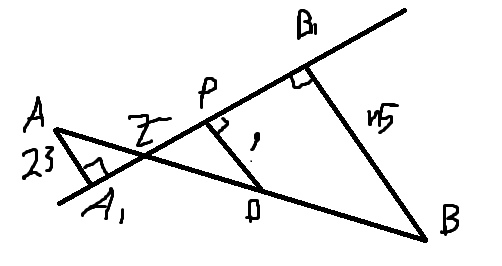
Пусть \( AB=x \)
Задача, очевидно, на подобие треугольников
\( \frac{OP}{BB1}=\frac{ZO}{ZB} \) откуда \( OP=\frac{BB1*ZO}{ZB} \)
\( \frac{BB1}{AA1}=\frac{ZB}{AZ}=\frac{45}{23} \)
\( AZ=\frac{23ZB}{45} \), а так как \( AZ+ZB=AB=x \), то \( ZB=\frac{45}{68}x \) и \( AZ=\frac{23}{68}x \)
\( ZO=AB-AZ-OB=x-\frac{23}{68}x-\frac{x}{2}=\frac{11}{68}x \)
\( OP=11 \) (подставляем все в синюю формулу)
Ответ: 11
