Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 45. Найдите радиус окружности.
Решение
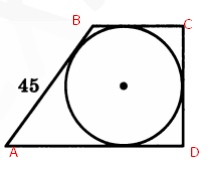
Так как в трапецию вписана окружность, то \( AB+CD=BC+AD \)
\( AB+BC+CD+AD=100 \) – по условию
\( CD=BC+AD-45 \)
\( 55-CD=BC+AD \) – из первого уравнения и подставляем вместо BC+AD выражение
\( CD=55-CD-45 \)
\( CD=5 \)
А радиус равен половине высоте трапеции, то есть 2,5
Ответ: 2,5
