Диагонали ромба равны 2√5 и 4√5. Найдите
радиус вписанной в ромб окружности.
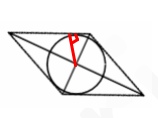
Решение
Найдем сторону ромба
\( a=\sqrt{(\sqrt{5}^2+(2\sqrt{5})^2)}=5 \) по т Пифагора
\( S_{ромба}=\frac{d_{1}*d_{2}}{2}=4*S_{треуг} \), а \( S_{треуг}=\frac{a*r}{2} \) (высота – это радиус вписанной окружности)
\( 4*\frac{5*r}{2}=\frac{8*5}{2} \)
\( r=2 \)
Ответ: 2
