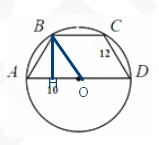
Трапеция АВСD вписана в окружность с диаметром АD. Найдите высоту трапеции, если радиус окружности равен 10, а боковая сторона трапеции равна 12.
Решение
Если трапеция вписана в окружность, то она равнобедренная!
А дальше уже решать нечего, достаточно вспонмить или вывести итак известную формулу
\( BH=h \)
\( AH=x \) тогда \( HO=10-x \)
И пользуемся теоремой Пифагора, для двух прямоугольных треугольников
\( 12^2=x^2+h^2 \)
\( 10^2=(10-x)^2+h^2 \)
вычтем из одного уравнения, второе и получим, что \( x=2,8 \)
значит \( h=9,6 \)
Ответ: 9,6
