В треугольнике ABC известно, что ∠C=90° и ∠B=24°. Найдите острый угол между его медианой CM и биссектрисой AL. Ответ дайте в градусах.
Решение
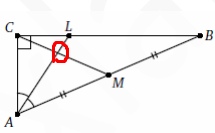
Для решения необходимо знать, что \( CM=0,5AB \), т.е половина гипотенузы, а значит треугольники \( ACM \) и \( CMB \) -р/б
\( ∠A=90-∠B=66 \)
\( ∠B=∠MCB=24 \)
\( ∠ALC=90-33=57 \)
\( ∠COL=180-57-24=99 \) – но это не острый угол, найдем смежных угол и получаем ответ
\( ∠LOM=180-99=81 \)
Ответ: 81
