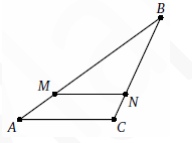
На сторонах AB и BC треугольника ABC выбраны точки M и N соответственно так, что MN || AC. Найдите AC, если NM =9, NC =4 и NB= AC.
Решение
Пусть \( AC=x \)
через подобие треугольников, выясняем, что \( \frac{MN}{AC}=\frac{BN}{BC} \) или
\( \frac{MN}{AC}=\frac{AC}{BC} \)
\( \frac{MN}{AC}=\frac{AC}{(BN+NC))} \)
\( \frac{MN}{AC}=\frac{AC}{(AC+NC)} \)
получаем уравнение
\( x^2-9x-36=0 \)
\( AC=12 \)
Ответ: 12
