В треугольнике ABC, в котором ∠A=30°, ∠B=105° проведена медиана CM.
Найдите ∠MCA . Ответ дайте в градусах.
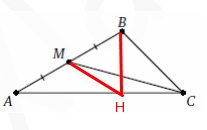
Решение
Задачка интересная:) И требует дополнительных построений, хотя я уверен, что можно и без них, но тогда понадобится уравнение медианы, а не каждый его помнит.
Проведем высоту \( BH \), и соединим \( MH \)
\( ∡С=180-∡A-∡B=45° \)
Обозначи \( BH=HC=a \) , так как треугольник \( BHC \) – прямоугольный и равнобедренный.
\( AB=2a \) – так как a – катет, лежащий против угла в 30 градусов..
\( MH=a \) – как медиана в прямоугольном равнобедренном треугольнике, это свойство очень легко доказывается:)
Получаем, что треугольник \( AMH \) – равнобедренный, значит \( ∡M=120° \), (\( ∡A=∡MHA=30° \))
\( △MHC \) – равнобедренный, так как \( MH=HC=a \)
\( ∡MHC=180°-30°=150° \), значит \( ∡HMC=∡MCA=\frac{180°-150°}{2}=15° \)
Ответ: 15
