К окружности радиуса 7 из точки P проведены касательные PA=PB=24. Найдите длину хорды AB.
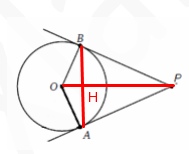
Решение
По т Пифагора \( OP=\sqrt{BO^2+BP^2}=25 \)
\( ∡OHB=90 \), так как OH – медиана, биссектрисса, высота в равнобедренном треугольнике \( OBA \)
\( BH=\frac{OB*BP}{OP}=6,72 \) – как высота прямоугольного треугольника, опущенная из прямого угла.
\( AB=2BH=13,44 \)
Ответ: 13,44
