В треугольнике АВС медианы АК и СР пересекаются под прямым углом в точке Q. Найдите длину медианы, проведенной из вершины В треугольника АВС, если известно, что АК=12, СР=9.
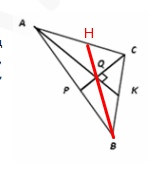
Решение
Медианы в точке пересечения делятся в отношении 2 к 1 считая от вершины, поэтому
\( CQ=2/3CP=6 \) и \( AQ=2/3AK=8 \)
\( AC=10 \) по т Пифагора
В прямоугольном треугольнике \( ACQ \) \( QH \) – медиана
\( QH=0.5AC=5 \) по свойству медианы в прямоугольном треугольнике
Тогда вся медиана равна, если QH – это 1/3 от нее, 15
Ответ: 15
