Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60 ,большее основание равно 12. Найдите радиус описанной
окружности этой трапеции.
Решение
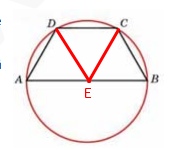
Проведем \( CE \) параллельно AD,
\( ADCE \) – ромб, все стороны равны
заметим, что \( CE=AD=CB \), то есть треугольник \( CEB \) – равнобедренный и так как \( ∡CEB=60 \), то он равносторонний.
\( AE=EB \)
Получаем, что точка \( E \) равноудалена от вершин и она является центром окружности, соотвественно радиус равен 6
Ответ: 6
