В равнобедренном треугольнике боковая сторона делится точкой касания со вписанной окружностью в отношении 8:5, считая от вершины, лежащей напротив основания. Найдите
основание треугольника, если радиус вписанной окружности равен 10.
Решение
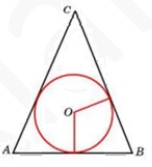
Главное знать – отрезки касательных, проведенных из одной точки, равны.
\( BC=AC=13x \)
\( AB=10x \)
\( S=pr \)
\( p=\frac{13x+13x+10x}{2}=18x \)
\( S=\sqrt{p(p-13x)(p-13x)(p-10x)} \) – по формуле Герона.
приравниваем два равенства и находим х
\( 10*18x=\sqrt{p(p-13x)(p-13x)(p-10x)} \)\( 180x=\sqrt{18x*5x*5x*8x} \)
\( 180x=60x^2 \)
\( x=3 \)
\( AB=10x=30 \)
Ответ: 30
