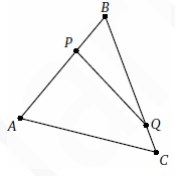
На сторонах AB и BC треугольника ABC выбраны соответственно точки P и Q так, что BP_PA=1:2 и BQ_QC=4:1. Найдите отношение площади четырёхугольника ACQP к
площади треугольника PBQ.
Решение
Вспомним формулу площади треугольника через угол
\( S=0.5absina \)
Пусть \( BP=x \), тогда \( AB=3x \)
Пусть \( BQ=4y \), тогда \( BC=5y \)
\( \frac{S_{BPQ}}{S_{ABC}}=\frac{0.5*BP*BQ*sinaB}{0.5*AB*BC*sinB}=\frac{BP*BQ}{AB*BC}=\frac{4}{15} \)
\( S_{BQP}=\frac{4}{15}S_{ABC} \)
\( S_{APQC}=S_{ABC}-\frac{4}{15}S_{ABC}=\frac{11}{15}S_{ABC} \)
\( \frac{S_{ACPQ}}{S_{BPQ}}=\frac{11}{4}=2,75 \)
Ответ: 2,75
