В равнобедренном треугольнике ABC с основанием AC боковая сторона равна 4√15 , sin BAC=0,25. Найдите длину высоты AH.
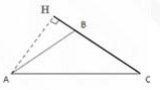
Решение
Так как треугольник равнобедренный, то углы при основании равны
\( sinBAC=sinBCA=0,25 \)
\( sinBCA=\frac{AH}{AC} \)
\( AH=0.25AC \)
Осталось найти AC
Проведем высоту BP
\( sinBCA=\frac{BP}{BC} \), \( BP=\sqrt{15} \)
По т Пифагора находим \( PC=\sqrt{BC^2-BP^2}=15 \)
BP – это еще и медиана, значит \( AC=2PC=30 \)
\( AH=0.25AC=0.25*30=7,5 \)
Ответ: 7,5
