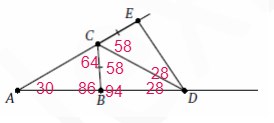
6. В треугольнике ABC известно, что A = 300 и B = 860. CD—биссектриса внешнего
угла при вершине C, причём D лежит на прямой AB. На продолжении стороны AC за
точку C выбрана точка E так, что CB = CE. Найдите ADE. Ответ дайте в градусах.
Решение
Просто находим все углы по т о сумме углов треугольника
Заметим, что треугольник \( CBD \) равен \( CED \) по двум сторонам и углу между ними, значит
\( ∡BDC=∡CDE \)
Ответ: 56
