Четырёхугольник ABCD вписан в окружность, причём
BC =CD. Известно, что угол ADC равен 93. Найдите, под
каким острым углом пересекаются диагонали этого
четырёхугольника. Ответ дайте в градусах.
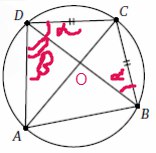
Решение:
По свойству пересекающихся хорд \( AO*OC=DO*OB \)
\( △ADO \) подобен \( △BCO \) (по двум пропорциональным сторонам и углу между ними\( ∡ADO=∡COB \))
Значит углы \( ∡OBC=∡DAO=a \)
Искомый угол \( ∡DOA=180°-(∡β+∡a) \)
\( ∡ADC=∡a+∡β \)
\( ∡DOA=180°-(∡β+∡a)=180°-93°=87° \)
Ответ: 87
