В трапеции ABCD (AD||BC) диагонали пересекаются в точке O. Площади
треугольников BCO и ADO равны, соответственно, 2 и 8. Найдите площадь трапеции.
Решение
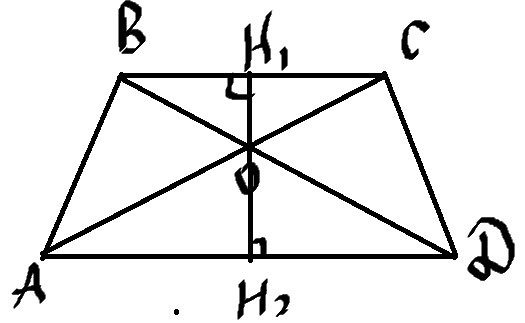
\( S=\frac{BC+AD}{2}*H_{1}H_{2} \)
\( k^2=\frac{S_{BOC}}{S_{AOD}} \) – отсюда \( k=0,5 \)
То есть стороны треугольника AOD в два раза больше, чем стороны треугольника BOC
Пусть \( BC=x \), тогда \( AD=2x \)
\( S_{BOC}=0.5*OH_{1}*BC \) – выражаем \( OH_{1}=\frac{4}{x} \)
\( S_{AOD}=0.5*OH_{2}*AD \) выражаем \( OH_{2}=\frac{8}{x} \)
Тогда \( H_{1}H_{2}=OH_{1}+OH_{2}=\frac{4+8}{x}=\frac{12}{x} \)
Находим площадь
\( S=\frac{x+2x}{2}*\frac{12}{x}=18 \)
Ответ: 18
