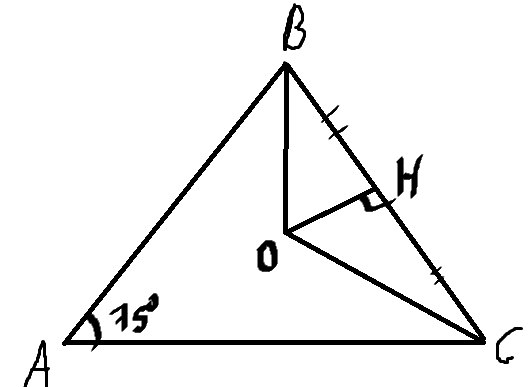
Около равнобедренного треугольника АВС с основанием АС и углом при основании
75°описана окружность с центром О. Найдите её радиус, если площадь треугольника
ВОС равна 16.
Решение
Я приведу два решения, одно легкое, другое сложное:)
1) \( ∡BAC=75° \) – является вписанный углом, а \( ∡BOC=150° \), как центральный угол
\( S_{BOC}=0.5*R^2*sin150° \) – выражаем R (BO=OC=R)
\( R^2=\frac{32}{sin150°}=64 \)
\( R=8 \)
2)\( S_{BOC}=\frac{1}{2}*OH*BC \) а OH найдем по т Пифагора \( OH=\sqrt{R^2-\frac{1}{4}*BC^2} \)
Значит \( S_{BOC}=\frac{1}{2}*\sqrt{R^2-\frac{1}{4}*BC^2}*BC \)
Теперь по т. синусов
\( 2R=\frac{BC}{sin75°} \) подставляем BC в предыдущее уравнение, и решаем уравнение 4 степени, ну и потом sin75 преобразовываем))
\( 2S_{BOC}=\sqrt{R^2-R^2\frac{1}{4}*4*sin^275°}*R*2*sin75° \) – все величины мы знаем, осталось возвести в квадрат и найти R.
\( 32^2=(R^2-R^2*sin^275°)*R^2*4*sin^275° \) – раскрываем скобки.
\( sin^275°=\frac{1-cos150°}{2} \)или \( sin75°=sin(30°+45°)=\frac{\sqrt{2}+\sqrt{6}}{4} \)
Ну а теперь дело техники) Упрощаем и находим R
\( R=8 \)
