Диагонали ромба относятся как 3:4. Периметр ромба
равен 200. Найдите высоту ромба.
Решение
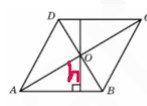
У ромба – все стороны равны, значит одна сторона равна 200_4=50
В точке пересечения O, диагонали делятся пополам.
Пусть \( OB=3x \) и \( AO=4x \), тогда можем найти AB
\( AB=\sqrt{AO^2+OB^2}=\sqrt{9x^2+16x^2}=5x \)
Значит \( 50=5x, x=10 \)
Треугольник \( AOB \) – прямоугольный , и его высота опущенная на гипотенузу AB равна
\( h=\frac{AO*OB}{AB}=\frac{3x*4x}{5x}=\frac{12x}{5}=\frac{12*10}{5}=24 \)
А высота ромба равна \( 2h \)
Ответ: 48
