В цилиндр вписана сфера. Площадь полной поверхности цилиндра равна 42. Найдите площадь поверхности сферы.
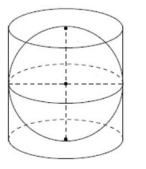
Решение
\( S_{пол.пов.цилиндра}=2S_{осн}+S_{б.п} \)
\( S_{осн}=\pi R^2 \) – окружности
\( S_{б.п}=2\pi R*2R \) в разрезе цилиндр – это прямоугольник со сторонами: длина окружности (\( 2\pi R \)) и высотой цилиндра 2R
\( S_{пол.пов.цинидра}=2\pi R^2+2\pi R*2R=6\pi R^2=42 \)
\( \pi R^2=7 \)
\( S_{пов.сферы}=4\pi R^2=4*7=28 \)
Ответ: 28
