В основании пирамиды лежит прямоугольник. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы 30° и 45°. Найдите диагональ прямоугольника, если высота пирамиды равна 4.
Решение
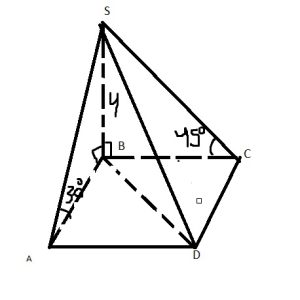
\( SB⟂(ABCD) \)
\( BC \) – проекция \( SC \) на \( ABCD \)
\( BC⟂DC \) (т.к прямоугольник)
Значит по т о 3-х перпендикулярах \( SC⟂DC \), значит \( ∠BCS \) – есть линейный угол двугранного угла \( ∠SBCD \)
Аналогично с \( ∠ABS \)
Пусть \( ∠BCS=45 \) и \( ∠ABS=30 \)
\( △SBC \) – прямоугольный и р/б значит \( BC=SB=4 \)
\( AB=\frac{SB}{tg30}=4\sqrt{3} \)
\( BD=\sqrt{AB^2+BC^2}=8 \)
Ответ: 8
