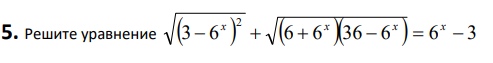
Решение
Пусть \( 6^x=t \), t>0
Ограничения
\( (6+t)(36-t)>=0 \) значит \( -6<=t<=36 \)
\( t-3>=0 \) значит \( t>=3 \)
Получаем, что \( 3<=t<=36 \)
\( |3-t|+\sqrt{(6+t)(36-t)}=t-3 \)
Модуль можно раскрыть однозначно со знаком минус с учетом \( 3<=t<=36 \)
\( \sqrt{(6+t)(36-t)}=0 \)
\( t=-6 \) – не подходит под условие
\( t=36 \)
\( 6^x=36 \)
\( x=2 \)
Ответ: 2
