Наугад выбирают два числа из отрезка [0;1]. Найдите вероятность того, что их сумма заключена между 1/4 и 1.
Решение
Пусть два числа это \( x \) и \( y \)
Рисуем два отрезка от 0 до 1, т.к из этих отрезков мы берем два числа, получим систему координат
\( \frac{1}{4}<=x+y<=1 \) – это из условия
Значит получаем некую область
\( y<=1-x \)
\( y>=1/4-x \)
Рисуем на координатной плоскости
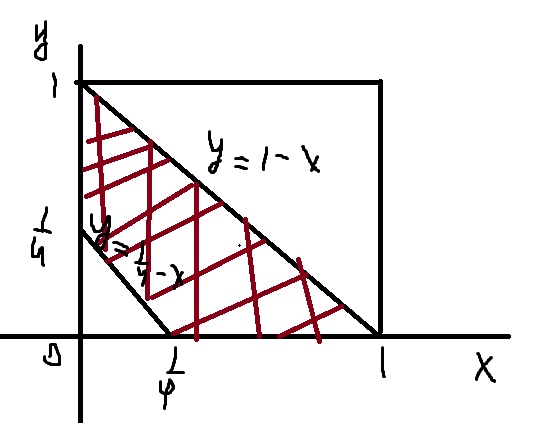
Красная область – оттуда мы должны брать числа \( x \) и \( y \), чтобы их сумма лежала в указанном отрезке
Нам нужно найти ее площадь и разделить на площадь большого квадрата (S=1)
Ее площадь равна из площадь большого прямоугольного треугольника вычитаем площадь маленького прямоугольного треугольника
\( P==\frac{\frac{1}{2}-\frac{1}{2}*\frac{1}{4}(\frac{1}{4}}{1}=\frac{15}{32}=0,46875 \)
Ответ: 0,46875
