В треугольнике АВС на сторонах АВ и ВС случайным образом выбираются точки А1
и С1 так, что отрезок А1С1 оказывается параллелен стороне АС. Найдите вероятность
того, что длина отрезка А1С1 окажется больше 3, если АС=5.
Решение
Задача на определение геометрической вероятности. Давайте вспомним о чем она:

Вероятность того, что точка окажется на отрезке \( CD \) равна отношению длин двух отрезков
\( P(Z)=\frac{CD}{AB} \) – будем применять данный факт
Теперь к самой задаче:
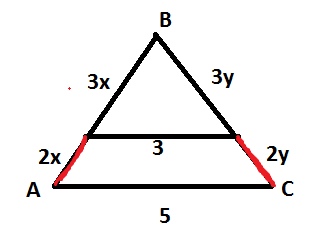
Мы выбираем любую точку на стороне AB или BC и проводим через нее линию параллельную стороне AC, по определению, показанном выше, вероятность того, что наша точка будет лежать на красненьком отрезке (а нам это нужно по условию) будет равна \( \frac{2x}{5x}=\frac{2y}{5y}=\frac{2}{5}=0,4 \)
Ответ: 0,4
