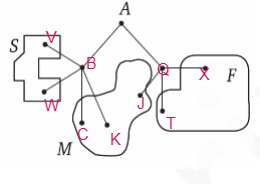
Аристарх Луков‐Арбалетов совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку S, другие—в поле F или в болото M. Найдите вероятность того, что Аристарх забредет в болото. Результат округлите до
сотых.
Решение
1) Вероятность того, что мы попадем в \( B \) равна 0.5 (думаю это понятно, всего путей 2, а нужный нам 1, 1/2=0.5)
Дальше из \( B \) нас устраивает попасть в \( C \) и \( K \) – это благоприятные исходы. Вероятность что мы туда попадем \( P(CK)=\frac{2}{4}=0.5 \) (всего дорог 4 из B)
Значит вероятность \( P(A-B-C,K)=0.5*0.5=0.25 \)
2) Из \( A \)мы можем попасть в \( Q \)Вероятность\( P(AQ)=0.5 \)
Из \( Q \) ведут три дороги, но нас устраивает попасть в \( J \) – одно благоприятное событие
\( P(Q-J,T)=\frac{1}{3} \) (всего дорог 3)
\( P(A-Q-J,T)=0.5*\frac{1}{3} \)
Значит искомая вероятность равна \( 0.25+0.5*\frac{1}{3}=0.416 \)
Ответ: 0,42
