В ромб ABCD вписана окружность, касающаяся стороны AD в точке F. Известно, что AF =4 ∙ FD. Найдите косинус острого угла ромба.
Решение
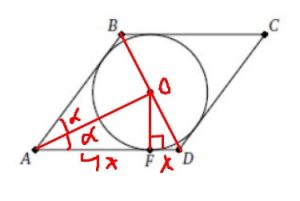
Треугольник \( AOD \) – прямоугольный, \( OF \) – высота в прямоугольном треугольнике, значит
\( OF^2=AF*FD=4x*x=4x^2 \)
\( OF=2x \)
\( AO=\sqrt{16x^2+4x^2}=2\sqrt{5}x \)
\( cos\alpha=\frac{4x}{2\sqrt{5}x}=\frac{2}{\sqrt{5}} \)
\( cos2\alpha=2cos^2\alpha-1=0,6 \)
Ответ: 0,6
