Окружность, вписанная в треугольник ABC, касается его стороны BC в точке N. Известно, что BN =15 и AC =17. Найдите периметр треугольника.
Решение
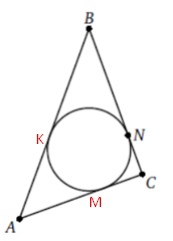
\( P=AB+AC+BC \)
\( P=AK+BK+BN+NC+AC \)
По св-ву касательных, проведенных из одной точки
\( AK=AM \)
\( NC=MC \)
\( BK=BN=15 \)
\( AC=AM+MC=AK+NC \)
Значит
\( P=17+17+15+15=64 \)
Ответ: 64
