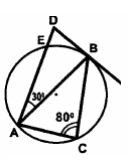
Найдите угол ADB (в градусах), изображенный на рисунке. Угол DAB равен 30, угол ACB равен 80. DB – касательная к окружности.
Решение
Пользуясь, тем, что угол между касательной и секущей, проведенными из одной точки, равен полуразности заключенных внутри него дуг, получаем
\( ∡ADB=\frac{1}{2}(200-60)=70 \)
(градусная мера дуги, на которую опирается угол, в два раза больше угла)
Дуга AB = 360-160=200
Дуга EB=30*2=60
Ответ: 70
