В параллелограмме ABCD АЕ – биссектриса, CF⊥AF AB=5 см, AD=12 см, AF=15 см. Найдите площадь треугольника АВЕ в квадратных сантиметрах.
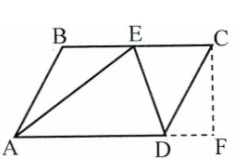
Решение
\( DF=AF-AD=3 \)
\( AE \) – биссектриса, значит треугольник \( ABE \) – равнобедренный.
\( CF=\sqrt{DC^2-DF^2}=4 \)
пусть \( sin(∠DAB)=sint \)
\( S_{ABCD}=CF*12=AB*AD*sint \)
\( sint=\frac{48}{60}=0,8 \)
\( S_{ABE}=0,5*AB*BE*sin(∠ABE) \)
\( ∠ABE=180-\frac{t}{2}-\frac{t}{2} \) (т.к биссектриса отсекает равные углы)
\( S_{ABE}=0,5*25*sin(\pi-t)=0,5*25*sint=0,5*25*0,8=10 \)
Ответ: 10
