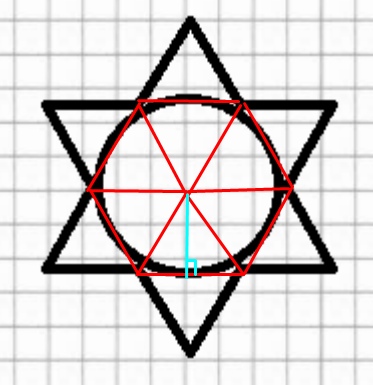
Найдите радиус окружности, изображенной на рисунке, считая сторону клетки равной √3
Решение
Замечаем, что радиус искомой окружности – это радиус описанной окружности около правильного шестиугольника
Высота одного правильного треугольника из рисунка равна \( 2,5\sqrt{3} \) (2,5 клетки)
\( h=\frac{a\sqrt{3}}{2} \) – высота правильного треугольника
\( 2,5\sqrt{3}=\frac{a\sqrt{3}}{2} \)
\( a=5=R \)
Ответ: 5
