На клетчатой бумаге изображён четырёхугольник ABCD. Найдите тангенс острого угла, под которым пересекаются его диагонали.
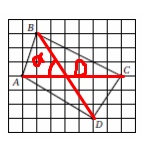
Решение
Находим длины сторон треугольника ABO по т пифагора из соотвествующих треугольников
\( AB=\sqrt{10}, BO=\sqrt{13}, AO=3 \)
по т косинусов
\( cosa=\frac{BO^2+AO^2-AB^2}{2*AO*BO}=\frac{2}{\sqrt{13}} \)
\( sina=\sqrt{1-cos^2a}=\frac{3}{\sqrt{13}} \)
\( tga=\frac{sina}{cosa}=1,5 \)
Ответ: 1,5
