Найти все значения х, при каждом из которых неравенство
\( (2-a)x^3+(1-2a)*x^2-6x+(5+4a-a^2)<0 \)
выполняется хотя бы при одном значении а, принадлежащем отрезку [‐1;2].
Решение
Скомпонуем все относительно \( a \)
\( a^2+(x^3+2x^2-4)a-(2x^3+x^2-6x+5)>0 \)
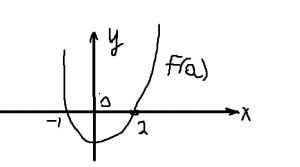
Чтобы решение было в [-1;2] нам нужно чтобы выполнялись два неравенства
\( f(-1)>0 \) и \( f(2)>0 \)
1) \( f(-1)<=0 \)
\( 1-x^3-2x^2+4-2x^3-x^2+6x-5>0 \)
\( x(x^2+x-2)<0 \)
Значит x принадлежит (-беск;-2) объединяя (0;1)
2) \( f(2)<=0 \)
\( 4+2x^3+4x^2-8-2x^3-x^2+6x-5>0 \)
\( x^2+2x-3>0 \)
\( (x+3)(x-1)>0 \)
значит x принадлежит (-беск;-3) объединяя с (1;+беск)
Ответ: \( (-∞;-2)⋃(0;1)⋃(1;+∞) \)
