Найдите все значения параметра a , при которых система неравенств
\( y>=x^2-ax+2 \)
\( y<=x+a \)
имеет ровно одно решение
Решение
Рассмотрим случай когда\( a=0 \)
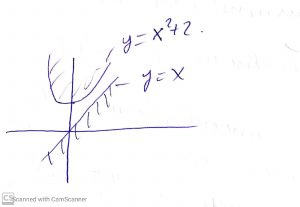
\( y>=x^2+2 \)
\( y<=x \)
Данная система не имеет решений
Значит рассматриваем \( a\neq0 \)
Чтобы решение было единственным, очевидно, прямая \( y=x+a \), должна быть касательной к параболе
Из этого найдем параметр a
\( y’=2x-a \)
\( y’=1 \)
Графики должны совпадать, т.е
\( 2x-a=1 \)
\( x=\frac{a+1}{2} \) – точка касания
И подставляем это в уравнения обеих функций (в т касания они равны)
\( \frac{a+1}{2}+a=(\frac{a+1}{2})^2-a*\frac{a+1}{2}+2 \)
Решая квадратное уравнение \( a^2+6a-7=0 \)
\( a=-7 \)
\( a=1 \)
Ответ: a=-7, 1
