Найдите все значения параметра а, при которых неравенство
\( cosx-2\sqrt{x^2+9}<=-\frac{x^2+9}{a+cosx}-a \)
имеет единственное решение.
Решение
\( cosx+a-2\sqrt{x^2+9}+\frac{x^2+9}{a+cosx}<=0 \)
Приведем все к общему знаменателю
\( \frac{(cosx+a)^2-2\sqrt{x^2+9}(cosx+a)+(x^2+9)}{a+cosx}<=0 \)
Замечаем квадрат разности
\( \frac{(cosx+a-\sqrt{x^2+9})^2}{cosx+a}<=0 \)
Т.к числитель неотрицательный, то чтобы неравенство выполнялось нас должно устраивать \( cosx+a>0 \)
Чтобы неравенство выполнялось \( cosx+a-\sqrt{x^2+9}=0 \)
\( cosx+a=\sqrt{x^2+9} \)
Из рисунка очевидно, что \( a=2 \) (из меня художник не очень)
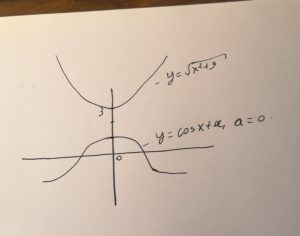
\( \sqrt{x^2+9}>=3 \), и чтобы было 1-решение, \( a=2 \)
Решение от пользователя rafack12@gmail.com

Ответ: a=2.
