1 июля планируется взять кредит в банке на сумму 300 тыс. рублей на некоторый
срок (целое число месяцев). Условия его возврата таковы:
‐ 15 числа каждого месяца долг возрастает на 10% по сравнению с началом
текущего месяца;
‐ с 16 по 28 число каждого месяца необходимо выплачивать часть долга.
‐ 1 числа каждого месяца долг должен быть на одну и ту же сумму меньше, чем
долг на 1 число предыдущего месяца.
На сколько месяцев был взят кредит, если известно, что сумма выплат за первый год
оказалась на 144 тыс. рублей больше, чем сумма выплат за второй год? Найдите
общую сумму выплат после полного погашения кредита.
Решение
Мы похожую задачу уже решали:) gdz-larin.ru/?p=1174
Рисуем ту же табличку с платежами
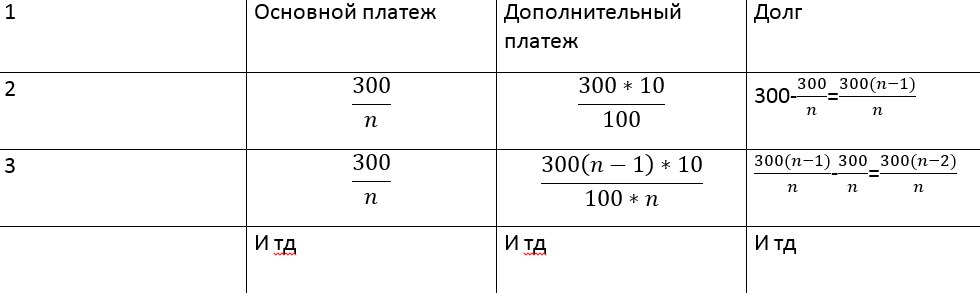
При желании можете продолжить эту таблицу, чтобы лучше усвоить задачу.
Найдем платежи за первый год (в году 12 месяцев)
\( S_{1}=\frac{300*12}{n}+\frac{300*10}{100}+\frac{30}{n}((n-1)+(n-2)+…+(n-11))=\frac{300*12}{n}+\frac{300*10}{100}+\frac{30}{n}(11n-66) \)
Найдем платежи за второй год
\( S_{2}=\frac{300*12}{n}+\frac{30}{n}((n-12)+…+(n-23))=\frac{300*12}{n}+\frac{30}{n}(12n-210) \)
\( S_{1}-S_{2}=144 \) – нам дано по условию
\( 30+\frac{30}{n}(11n-66)-\frac{30}{n}(12n-210)=144 \)
Отсюда находим \( n=30 \) – ура!
Теперь найдем сумму платежей за 30 месяцев
\( S_{30}=\frac{a_{1}+a_{30}}{2}*30 \)
\( a_{1}=\frac{300}{30}+\frac{300*10}{100}=40 \)
\( a_{2}=\frac{300}{30}+\frac{30*29}{30}=39 \)
\( a_{30}=a_{1}+(30-1)*d \)
\( d=a_{2}-a_{1}=39-40=-1 \)
\( a_{30}=40-29=11 \)
\( S_{30}=\frac{40+11}{2}*30=765 \)
Ответ: 30 месяцев, 765 тысяч.
