На стороне АВ выпуклого четырехугольника АВCD выбрана точка М так, что \( ∠AMD=∠ADB \) и \( ∠ACM=∠ABC \) Утроенный квадрат отношения расстояния
от точки А до прямой CD к расстоянию от точки С до прямой AD равен 2, СD = 20.
а) Докажите, что треугольник ACD равнобедренный.
б) Найдите длину радиуса вписанной в треугольник АСD окружности.
Решение
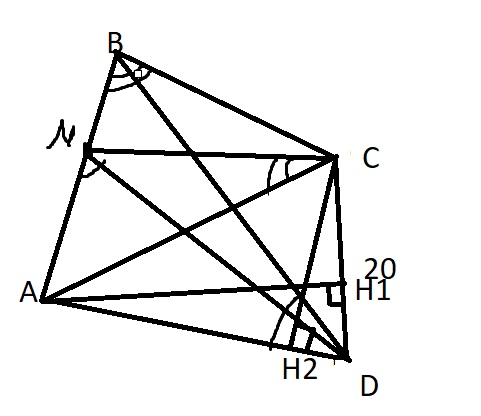
а) Заметим, что \( △ADM \) подобен \( △ABD \) по 2-м углам
\( \frac{AD}{AM}=\frac{AB}{AD} \), откуда \( AM*AB=AD^2 \)
Так заметим, что \( △ACM \) подобен \( △ABC \) по 2-м углам
\( \frac{AC}{AB}=\frac{AM}{AC} \), откуда \( AC^2=AM*AB \)
А значит \( AD=AC \) и треугольник ACD – р/б ч.т.д
Б) Нам дано \( 3*(\frac{AH_{1}}{CH_{2}})^2=2 \)
\( \frac{AH_{1}}{CH_{2}}=\sqrt{\frac{2}{3}} \)
\( S_{ADC}=0.5*CD*AH1=0.5*AD*CH2 \)
\( 20*AH1=AD*CH2 \)
\( AD=20*\sqrt{\frac{2}{3}} \)
\( r=\frac{S}{p} \), где \( p \) -полупериметр
\( p=10+20\sqrt{\frac{2}{3}} \)
\( AH_{1}=\sqrt{AD^2-DH1^2}=10\sqrt{\frac{5}{3}} \)
\( S=0.5*20*10\sqrt{\frac{5}{3}} \)
Значит
\( r=\frac{10\sqrt{\frac{5}{3}}}{1+10\sqrt{\frac{2}{3}}} \) – это ответ, но можно, конечно, привести к красивому виду. (кто как хочет)
Ответ: \( r=\frac{10\sqrt{\frac{5}{3}}}{1+10\sqrt{\frac{2}{3}}} \)
