Сторона АВ треугольника АВС равна 3, ВС=2АС, Е – точка пересечения
продолжения биссектрисы CD данного треугольника с описанной около него
окружностью, причем DE=1.
А) Докажите, что AE || BC
Б) Найдите длину стороны АС
Решение
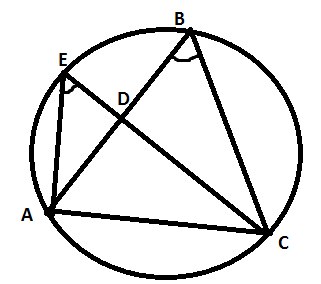
А) По свойству биссектриссы: \( \frac{BD}{AD}=\frac{BC}{AC}=\frac{2}{1} \)
Так как AB=3, то \( AD=1 \), \( BD=2 \)
Замечаем, что треугольник \( EDA \) – р/б
\( ∡AEC=∡ABC \) – так как опираются на одну дугу АС
\( ∡EDA=∡BDC \) – как вертикальный
Значит \( △EDA \) подобен \( △BDC \)
\( △BDC \) – р/б тоже
\( BD=DC=2 \)
\( ∡DBC=∡BCD=∡AED=∡DAE \) – эти углы накрест лежащие при прямых BC и AE
Получаем, что \( AE \) параллельно \( BC \)
Б) По т косинусов для \( △ADC \)
\( DC^2=AD^2+AC^2-2AC*cosA \)
\( 4=1+AC^2-2AC*cosA \)
Отсюда \( 2AC*cosA=AC^2-3 \) (*)
По т косинусов для \( △ABC \)
\( BC^2=AB^2+AC^2-AB*AC*cosA \)
\( 4AC^2=9+AC^2-2*3*AC*cosA \)
Подставляем (*)
\( 4AC^2=9+AC^2-3AC^2+9 \)
\( AC=\sqrt{3} \)
Ответ: \( \sqrt{3} \)
