В треугольнике АВС точка D есть середина АВ, точка Е лежит на стороне ВС,
причем BE=1/3*BC. Отрезки АЕ и CD пересекаются в точке О.
А) Доказать, что AO/OE=3/2
Б) Найти длину стороны АВ, если АЕ=5, ОС=4, а угол АОС равен 120
Решение
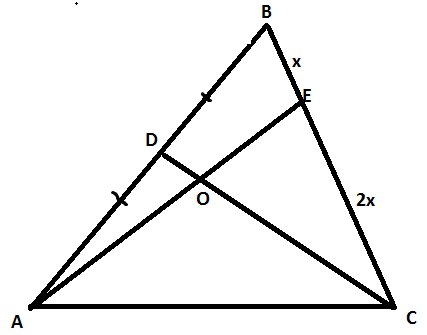
а) По т Менелая
\( \frac{BD}{AD}*\frac{AO}{OE}*\frac{EC}{BC}=1 \)
\( 1*\frac{AO}{OE}*\frac{2}{3}=1 \)
\( \frac{AO}{OE}=\frac{3}{2} \)
Б) так как AE=5, то \( AO=3 \), \( OE=2 \)
по т. Менелая \( \frac{BE}{EC}*\frac{OC}{DO}*\frac{AD}{AB}=1 \)
\( \frac{OC}{DO}=4 \)
\( DO=\frac{1}{4}*OC=1 \)
\( ∡AOD=180-120=60 \)
по т. косинусов из треугольника AOD
\( AD^2=DO^2+AO^2-2DO*AO*cos60 \)
\( AD=\sqrt{7} \)
\( AB=2\sqrt{7} \)
Ответ: \( 2\sqrt{7} \)
