Треугольник АВС (АВ<АC) вписан в окружность. На стороне АС отмечена точка Е
так, что АЕ=АВ. Серединный перпендикуляр к отрезку СЕ пересекает дугу ВС, не
содержащую точки А, в точке К.
А) Докажите, что АК является биссектрисой угла ВАС.
Б) Найдите площадь четырехугольника АВКЕ, если известно, что АВ=5, АС=11, ВС=10.
Решение
Сделаем рисунок, но соединим отрезки EK, KC, BK, BE
Проведем наш перпендикуляр KF
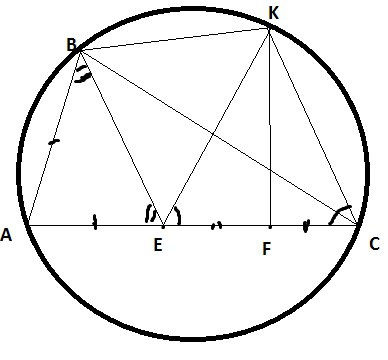
Заметим, что треугольник KEC-равнобедренный, т.к KF – медиана и высота
Пусть \( ∡KEF=∡KCF=∡w \)
Пусть \( ∡ABE=∡AEB=∡B \)
\( ∡BEK=180-∡b-∡w \)
У нас появился вписанный четырехугольник ABKC
\( ∡ABK+∡ACK=180 \)
\( ∡ABK=180-∡w \)
\( ∡EBK=180-∡w-∡B \)
Получаем два равных угла, значит треугольник BKE – равнобедренный (т.к углы при основании равны)
\( BK=KE \)
\( △ABK=△AEK \) – по трем сторонам, соотвественные углы равны \( ∡BAK=∡KAE=∡a \)
\( AK \) – биссектриса угла BAC, так как делит угол пополам, ч.т.д.
Б) мы доказали равенство треугольников в пункте А
\( S_{ABKE}=2S_{AKE} \)
\( △ABC \) по т косинусов
\( BC^2=AB^2+AC^2-2AB*AC*cos2a \)
\( cos2a=\frac{23}{55} \)
\( cos^2a-sin^2a=\frac{23}{55} \)
\( 1-2sin^2a=\frac{23}{55} \)
\( sina=\frac{4}{\sqrt{55}} \)
\( cosa=\frac{\sqrt{39}}{\sqrt{55}} \)
\( tga=\frac{4}{\sqrt{39}} \)
Из треугольника AKF
\( KF=AF*tga=\frac{32}{\sqrt{39}} \)
\( S_{EKF}=0.5*3*\frac{32}{\sqrt{39}}=\frac{48}{\sqrt{39}} \)
\( △AKE \) и \( △KEF \) имеют общую высоту
\( \frac{S_{AKE}}{S_{KEF}}=\frac{AE}{EF}=\frac{5}{3} \)
\( S_{AKE}=S_{KEF}*\frac{5}{3}=\frac{48}{\sqrt{39}}*\frac{5}{3}=\frac{80}{\sqrt{39}} \)
\( S_{ABKE}=2S_{AKE}=\frac{160}{\sqrt{39}} \) – это и есть ответ
