Четырехугольник ABCD вписан в окружность с центром в точке О. Радиус АО
перпендикулярен радиусу ОВ, а радиус ОС перпендикулярен радиусу OD.
А) Докажите, что ВС|| AD
Б) Найдите площадь треугольника АОВ, если длина перпендикуляра, опущенного из
точки С на AD, равна 9, а длина отрезка ВС в два раза меньше длины отрезка AD.
Решение
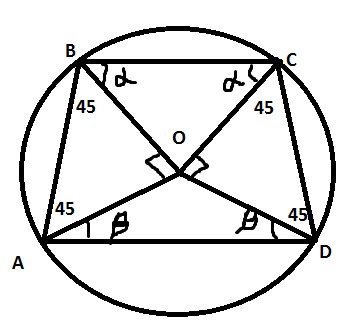
\( △BOD \) и \( △OCD \) прямоугольные и равнобедренные
Пусть \( ∡OBC=a \), \( ∡OAD=B \)
\( ∡ADC+∡ABC=180 \) (т.к ABCD вписан в окружность)
\( ∡a+45+∡B+45=180 \), отсюда \( ∡a+∡B=90 \)
\( ∡ADC+∡DCB=∡B+45+∡a+45=∡B+∡a+90=180 \), а это односторонние углы при прямых BC и AD, секущей DC
Значит ВС || AD ч.т.д.
б)
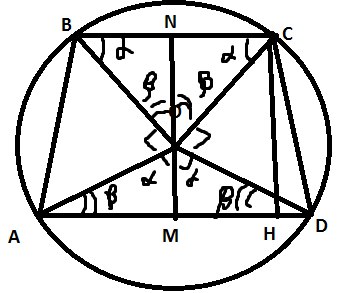
\( ∡BON=90-∡a=∡B \)
\( ∡AOM=90-∡B=∡a \)
\( △NCO=△OMD \) (по второму признаку)
\( △BCO=△AOD \) (по второму признаку)
значит и \( △BCO=△AOD \)
\( \frac{NO}{OM}=\frac{AD}{BC}=\frac{2}{1} \)
\( NO=2OM \), так как \( NM=9 \), то \( OM=3 \), а \( NO=6 \)
\( AO=\sqrt{AM^2+OM^2} \)
\( AM=NO=6 \)
\( AO=\sqrt{36+9}=\sqrt{45} \)
\( S_{AOB}=0.5*BO*AO=0.5*AO^2=22.5 \)
Ответ: 22.5
