Из середины D гипотенузы АВ прямоугольного треугольника АВС проведен луч,
перпендикулярный к гипотенузе и пересекающий один из катетов. На нем отложен
отрезок DE, длина которого равна половине отрезка АВ. Длина отрезка СЕ равна 1 и
совпадает с длиной одного из катетов.
А) Докажите, что угол АСЕ равен 45 градусов
Б) Найдите площадь треугольника АВС
Решение
Рисуем прямоугольный треугольник, опишем вокруг него окружность (центр описанной окружность вокруг прямоугольного треугольника лежит на середине гипотенузы)
а) Соединим отрезки EC и EB
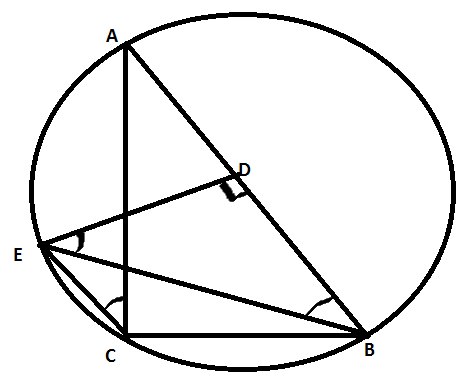
Заметим, так как ED равняется половине гипотенузы (то есть радиусу окружности), то точка E будет лежать на окружности.
\( △EDB \) – прямоугольный и равнобедренный по условию, значит углы при основании по 45.
\( ∡ABE \) опирается на дугу AE, \( ∡ACE \) тоже опирается на дугу AE, делаем вывод, что \( ∡ACE=∡ABE=45 \)
б) Один из катетов равен 1, возьмем для удобства BC=1
Рассмотрим треугольник \( EBC \), мы знаем, что он равнобедренный (по условию) и его тупой угол \( ∡ECB=90+45=135 \)
По т. косинусов \( EB^2=EC^2+BC^2-2EC*BC*cos135 \)
\( cos(135)=cos(90+45)=-sin45 \)
\( EB^2=2+\sqrt{2} \)
Проведем в треугольнике EDB медиану DH, медиана в прямоугольном, равнобедренном треугольнике равна половине стороны основания \( DH=0.5EB \)
\( sin45=\frac{DH}{DB} \) отсюда \( DB=\sqrt{\frac{2+\sqrt{2}}{2}} \)
\( AB=2DB=2*\sqrt{1+\frac{\sqrt{2}}{2}} \)
\( AC=\sqrt{4+2\sqrt{2}-1}=\sqrt{3+2\sqrt{2}} \)
\( S=0.5*BC*AC=0.5*\sqrt{1+2\sqrt{2}+\sqrt{2}^2}=0.5\sqrt{(1+\sqrt{2})^2}=\frac{1+\sqrt{2}}{2} \) (тут я выделил полный квадрат)
Ответ: \( \frac{1+\sqrt{2}}{2} \)
