Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка
R на боковой стороне CD выбрана так, что 2CD=3RD. Прямые AR и PD
пересекаются в точке Q , AD=2BC.
А) Докажите, что точка Q – середина отрезка AR
Б) Найдите площадь треугольника APQ.
Решение
Сделаем рисунок…
а) Частый прием в 16 задачах про трапецию, это продолжать стороны до пересечения и находить пары подобных треугольников. Так мы и сделаем.
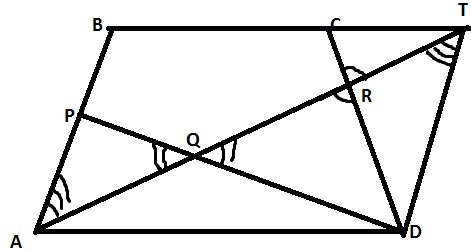
Продолжим \( AR \) и \( BC \) до пересечения в точке \( T \), соединим \( TD \)
\( △ARD \) подобен \( △CRT \) ( по 2-м углам)
\( \frac{CT}{AD}=\frac{CR}{RD}=0.5=\frac{RT}{AR} \) отсюда \( AR=2RT \), если \( AD=y \), то \( CT=y \)
Получаем, что \( BT=AD \) (у нас еще по условию AD=2BC) и эти стороны параллельны по условию, значит \( ABTD \) -параллелограмм.
\( △APQ \) подобен \( △TQD \) ( по 2-м углам)
\( k=\frac{AP}{TD}=\frac{1}{2}=\frac{AQ}{QT} \), отсюда \( QT=2AQ \)
Пусть \( AQ=z \), тогда \( QT=QR+RT=2z \), \( RT=2z-QR \)
Мы уже знаем что \( AR=2RT \
значит \( z+QR=2RT \) подставляем RT, \( z+QR=4z-2QR \), получаем, что \( QR=z \) т.е \( Q \) – середина, ч.т.д
б) \( \frac{S_{APQ}}{S_{TQD}}=k^2=\frac{1}{4} \), т.е мы можем найти площадь \( S_{TQD} \) и задача решена, к этому мы и идем.
\( S_{ABTD}=BT*h \), h – какая-то высота, нам неизвестная
\( S_{CTD}=0.5CT*h=0.25*BT*h \) (BC=CT -это мы уже доказывали)
Значит \( S_{ABCD}=\frac{3}{4}S_{ABTD}=30 \) отсюда \( S_{ABTD}=40 \)
\( S_{ATD}=0.5S_{ABTD}=20 \)
\( S_{QTD}=\frac{2}{3}S_{ATD} \) (т.к AT – 3 части, а QT – 2 части -а это основания треугольников, а площади треугольник относятся как основания, т.к высоты у них равны)
\( S_{QTD}=\frac{40}{3} \)
\( S_{APQ}=\frac{1}{4}*S_{QTD}=\frac{1}{4}*\frac{40}{3}=\frac{10}{3} \)
Ответ: \( \frac{10}{3} \)
