Две окружности касаются друг друга внешним образом в точке К. Прямая р
касается первой окружности в точке М, а второй – в точке N.
а) Докажите что расстояние от точки К до прямой р равно \( \frac{MK*KN}{MN} \)
б) Найдите площадь треугольника MNK, если известно, что радиусы окружностей
равны соответственно 12 и 3.
Решение
Сделаем рисунок
А) Проведем прямую p, проведем радиусы в точку касания, проведем расстояние от K до прямой p \( KZ \), проведем общую касательную \( KA \)
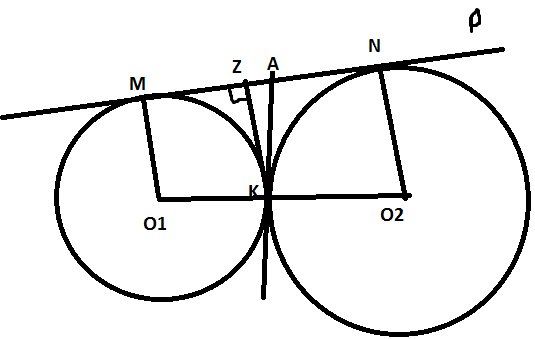
\( AM=AK \) и \( AN=AK \) (отрезки касательных к окружности, проведенные из одной точки равны между собой), значит точка \( A \) – середина и \( AK \) – медиана.
Рассмотрим треугольник \( MKN \) – в нем медиана AK равна половине стороны к которой она проведена, значит треугольник \( MKN \) – прямоугольный
Треугольник \( MKZ \) подобен \( MKN \) ( оба прямоугольные, угол M – общий)
Запишем подобие
\( \frac{KZ}{KN}=\frac{MK}{MN} \) отсюда \( KZ=\frac{MK*KN}{MN} \) – ч.т.д!
Б) \( O_{1}M∥KZ∥O_{2}N \) – т.к они перпендикулярны к одной прямой.
\( O_{1}O_{2}MN \) – трапеция, проведем высоту \( O_{1}E \)
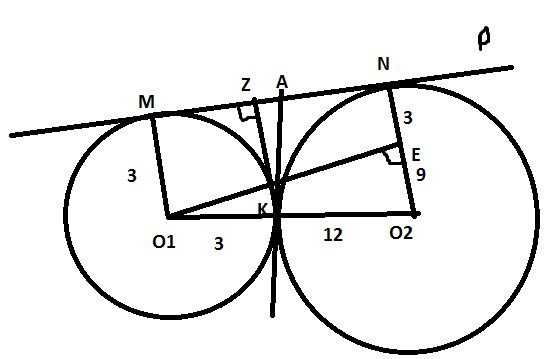
\( O_{1}E=\sqrt{O_{1}O_{2}^2-EO_{2}}=\sqrt{15^2-9^2}=12 \)
\( MNO_{1}O_{2} \) – прямоугольник, значит \( MN=O_{1}E \)
\( S_{MNK}=0.5*KZ*MN \), осталось найти KZ,
\( KZ=\sqrt{MD*DN} \) – как высота в прямоугольном треугольнике
По обобщенной теореме Фалеса \( \frac{O_{1}K}{KO_{2}}=\frac{MZ}{ZN}=\frac{1}{4} \)
Значит всего частей 5, получаем, что \( MZ=\frac{12}{5} \), а \( ZN=\frac{12}{5}*4=\frac{48}{5} \)
\( KZ=\sqrt{MD*DN}=\sqrt{\frac{12}{5}*\frac{12}{5}*4}=\frac{24}{5} \)
\( S_{MNK}=0.5*12*\frac{24}{5}=28,8 \)
Ответ: 28,8
