На стороне BC треугольника ABC отмечена K точка так, что AK = 4, ВК = 9, КС = 3.
Около треугольника ABK описана окружность. Через точку C и середину D стороны AB
проведена прямая, которая пересекает окружность в точке P, причем CP > CD и
APB=BAC
а) Докажите подобие треугольников АВС и АКС;
б) Найдите DP.
Решение
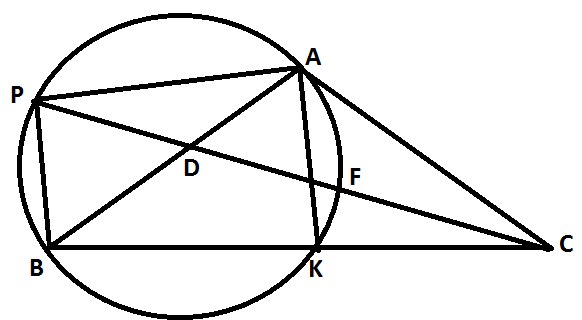
Пункт А
\( BPAK \) – вписанный четырехугольник, по свойству: противоположные углы в сумме равны 180 градусов
\( ∡APB+∡AKB=180° \) (1)
\( ∡AKB+∡AKC=180° \) (2)
Вычтем из (1) (2) получим, что \( ∡APB=∡AKC=∡BAC \)
\( △ABC \) подобен \( △AKC \) по двум углам, т.к (\( ∡C \)- общий, \( ∡AKC=∡BAC \))
Пункт Б
\( \frac{AB}{AK}=\frac{BC}{AC}=\frac{AC}{KC} \), выразим AC
\( AC^2=36 \) значит \( AC=6 \)
\( \frac{AB}{4}=\frac{6}{3} \) отсюда \( AB=8 \)
\( CD \) – медиана по условию, мы можем найти ее, т.к знаем все стороны
\( BC=9+3=12 \)
\( CD^2=0.5(AC^2+BC^2)-AD^2=0.5(36+144)-16=74 \) – по свойству медианы.
\( CD=\sqrt{74} \)
По свойству секущих \( CF*CP=CK*BC=36 \)
По свойству пересекающихся хорд \( PD*DF=BD*DA=16 \)
Пусть\( PD=x \), тогда \( CF=CD-DF=\sqrt{74}-\frac{16}{x} \)
\( CP=CD+DP=\sqrt{74}+x \)
Подставим все в уравнение \( (\sqrt{74}-\frac{16}{x})*(\sqrt{74}+x)=36 \) раскрываем скобки и решаем квадратное уравнение
\( \sqrt{74}x^2+22x-16\sqrt{74}=0 \)
\( D=484+64*74=5220=6\sqrt{145} \)
\( x=\frac{-22+6\sqrt{145}}{2*\sqrt{74}}=\frac{-11+3\sqrt{145}}{\sqrt{74}} \) – это и есть ответ
