Два борта бильярдного стола образуют угол 7, как указано на рисунке. На столе
лежит бильярдный шар A, который катится без трения в сторону одного из бортов под
углом 113. Отражения от бортов абсолютно упругие. Сколько раз шар отразится от
бортов?
Не знаю какое отношение эта задача имеет к ЕГЭшной планиметрии.
При решении будет пользоваться законом отражения света, вспомним их:
1. Луч падающий, луч отраженный и перпендикуляр к границе раздела лежат в одной плоскости (плоскости падения) – это нам не понадобиться, но для общего развития можно и запомнить)
2. Угол падения равен углу отражения – это мы будем использовать при решении задачи.
Решение
Сделаем рисунок, чтобы увеличить кликните по фотке.
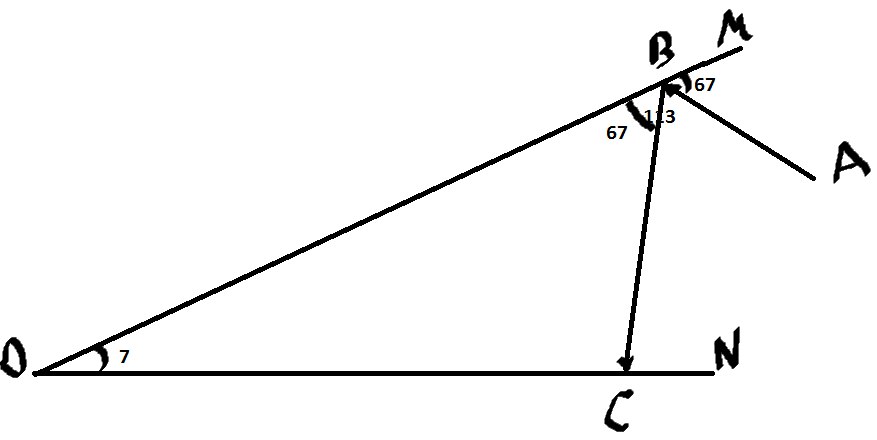
\( ∡OBA=113° \), а \( ∡BMA=67° \) (смежные)
Тогда по закону отражения \( ∡OBC=67° \)
Внешний угол треугольника
Тогда \( ∡BCN=67°+7°=74° \)
Рисуем дальше
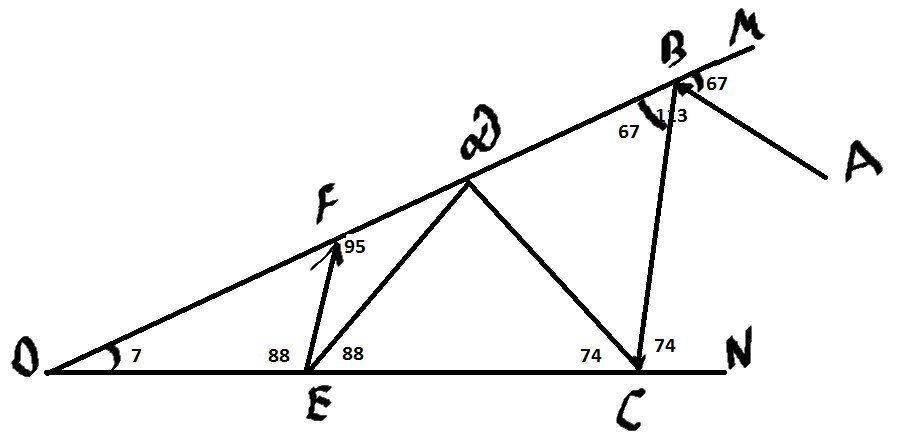
Угол падения равен углу отражения, тогда \( ∡DCO=74° \)
\( ∡CDM=74°+7°=81° \), тогда \( ∡EDO=81° \)
\( ∡DEC=7°+81°=88° \) и “Угол падения равен углу отражения” значит \( ∡OEF=88 \)
Внешний угол \( ∡EFD=95° \)- он тупой, значит дальше шар будет лететь в “обратную сторону”.
Сделаем новый рисунок, мы не забываем, что шарик уже отразился 5 раз!
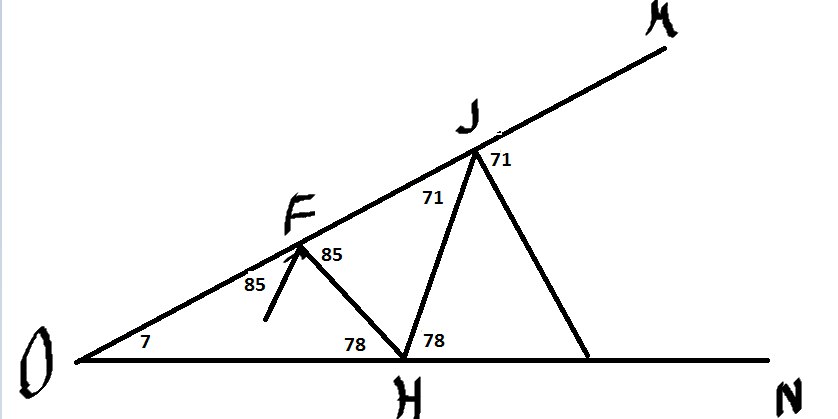
\( ∡OFE=180°-96°=85° \) по закону отражения \( ∡HFJ=85° \)
\( ∡OHF=84°-7°=78° \) по закону отражения \( ∡JHN=78° \)
Идем дальше
\( ∡OJH=78°-7°=71° \)и тд.
Мы видим, что угол постоянно уменьшается на 7. Тогда в 15 раз угол уже будет равен 15 градусам (85-70=15), а в 17 раз отражения угол будет равен 1 градусам и шарик больше не коснется борта.
Ответ: 17
