В трапеции ABCD BC II AD, ∠ABC=90° . Прямая, перпендикулярная
стороне CD, пересекает сторону АВ в точке М, а сторону CD – в точке N.
а) Докажите подобие треугольников АВN и DCM
б) Найдите расстояние от точки А до прямой ВN, если МС = 5, ВN = 3, а расстояние от
точки D до прямой МС равно 6.
Решение
Изобразим рисунок
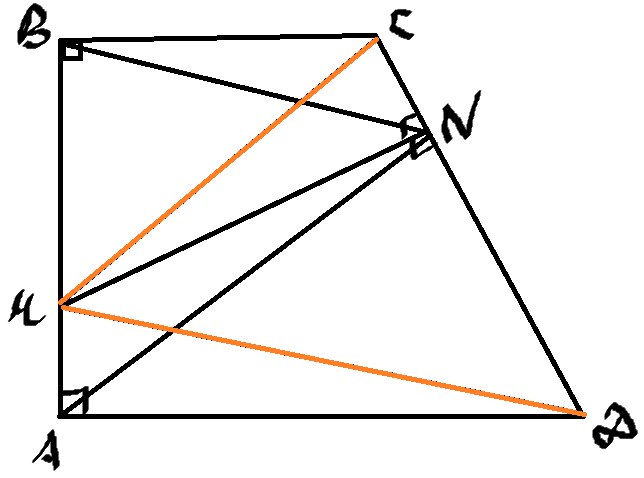
Я специально выделил две прямые MC и MD, сейчас поймете зачем.
Используем утверждение: Если отрезок виден из двух точек под одним углом, то такие точки лежат на одной окружности. А если еще эти углы прямые, то отрезок будет диаметром окружности.
Итак, отрезок MC виден из точек B и N под одним углом (90), значит около четырехугольника MBCN можно описать окружность.
Отрезок MD виден из точек A и N под одним углом, значит эти точки лежат на одной окружности.
Покажем эти окружности
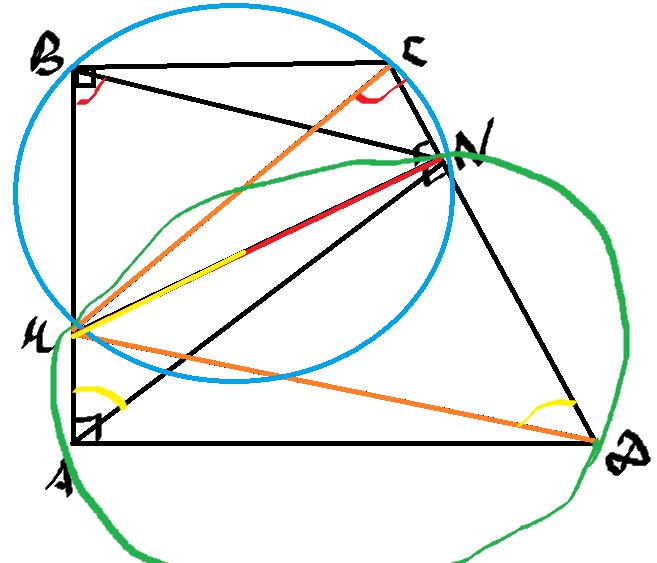
Заметим, что углы \( ∡MBN=∡MCN \) и \( ∡MAN=∡MDN \) так как опираются на одну и ту же дугу
Значит \( △ABN \) подобен \( △DCM \) по двум углам
Пункт Б
Проведем соответствующие высоты.
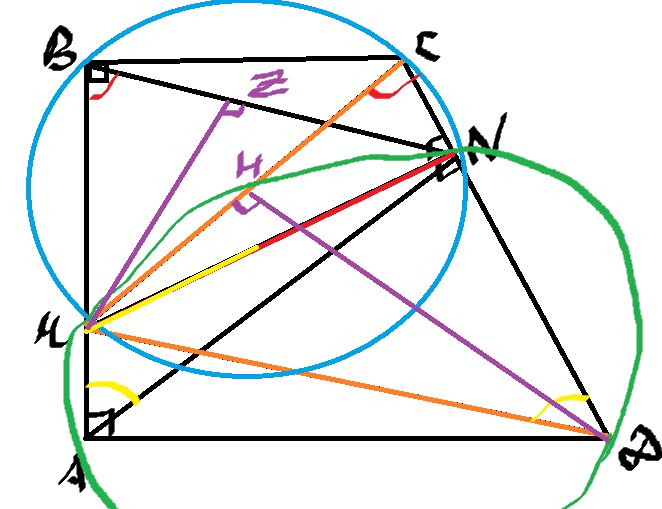
Пункт А часто помогает решению пункта Б:)
Как же мы используем подобие? А вот как
В подобных треугольниках отношение высот равно отношению соответствующих оснований.
Мы имеем \( \frac{BN}{MC}=\frac{AZ}{DH} \) отсюда находим нужное нам AZ, т.к нам все известно)
\( \frac{3}{5}=\frac{AZ}{6} \) значит \( AZ=3.6 \)
Ответ: 3.6
