Высоты равнобедренного треугольника АВС с основанием АС пересекаются в
точке Н, угол В равен 30 градусов. Луч СН второй раз пересекает окружность ,
описанную вокруг треугольника АВН, в точке К.
а) Докажите, что ВА – биссектриса угла КВС.
б) Отрезок ВС пересекает окружность в точке Е. Найдите ВЕ, если АС = 12.
Решение
Изобразим рисунок
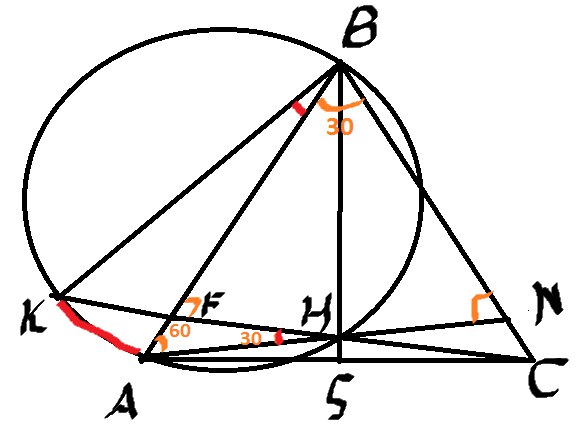
Не пугаемся углов. Сейчас все расскажу.
Пункт А
Если BA делит угол KBC пополам, то это биссектриса, докажем это (то есть угол должен быть KBA=30)
Из треугольника \( ABN \) \( ∡BAN=90°-∡ABC=90°-30°=60° \)
Из треугольника \( AFH \) найдем \( ∡AHF=90°-BAH=90°-60°=30° \)
Углы \( ∡KBA=∡FHA=30° \) так как опираются на одну и туже дугу
Получаем что BA – биссектриса угла KBC.
Пункт Б
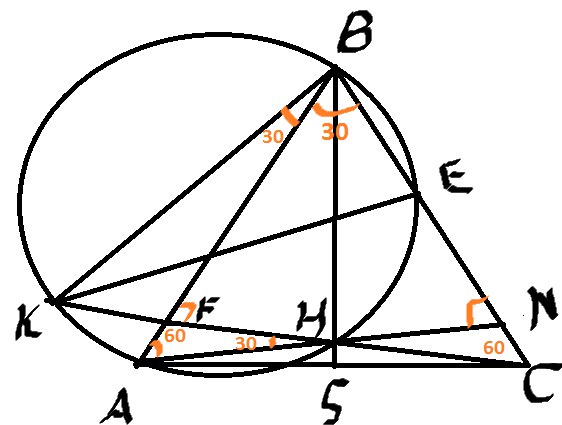
Углы \( ∡BKF=∡FAH=60° \) так как опираются на одну и ту же дугу.
Заметим, что \( △KBC \) – равносторонний, так как все углы равны 60. \( ∡C=180°-60°-60°=60° \)
А в равностороннем треугольнике биссектриса BA – это еще и высота и медиана!
То есть \( KF=FC \)
\( △KFA=△AFC \) (по двум катетам) значит \( KA=AC=12 \)
По теореме синусов для \( △KBA \) имеем:
\( 2R=\frac{KA}{sin30°}=\frac{12}{sin30°} \) отсюда \( R=12 \)
Из треугольника \( KBE \) по теореме синусов имеем:
\( 2R=\frac{BE}{sin∡BKE} \) – остается найти этот угол и задача решена:)
\( ∡EKH=∡EBH=15° \) – как углы, опирающиеся на одну и ту же дугу.
\( ∡BKE=∡BKC-∡EKH=60°-15°=45° \)
Все нашли! теперь подставляем в формулу и находим BE
\( BE=2R*sin45°=2*12*\frac{\sqrt{2}}{2}=12\sqrt{2} \)
Ответ: \( 12\sqrt{2} \)
