Две окружности касаются внутренним образом в точке K. Пусть AB – хорда большей
окружности, касающаяся меньшей окружности в точке L.
а) Докажите, что KL – биссектриса угла AKB.
б) Найдите длину отрезка KL, если известно, что радиусы большей и меньшей окружностей
равны соответственно 6 и 2, а угол АKB равен 90°
Решение
а) Сделаем рисунок (чтобы увеличить кликните по фотографии)
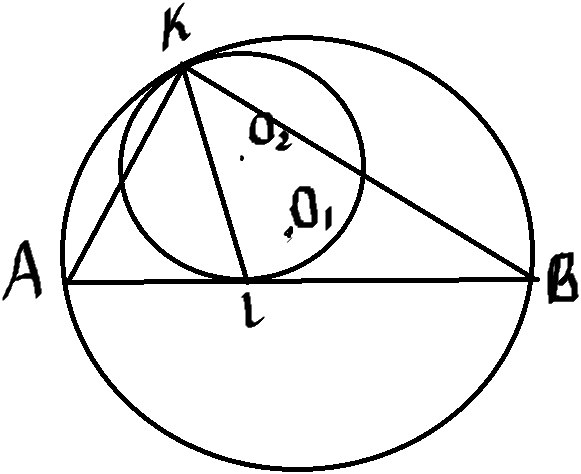
Чтобы доказать, что KL – биссектриса, докажем, что \( ∡AKL=∡LKB \)
Продолжим KL до пересечения с окружностью, M-точка пересечения
Построим диаметр большей окружности MN.
Если две окружности касаются, то их центры и точка касания лежат на одной прямой. Соединим KO1 до пересечения с дугой AB.
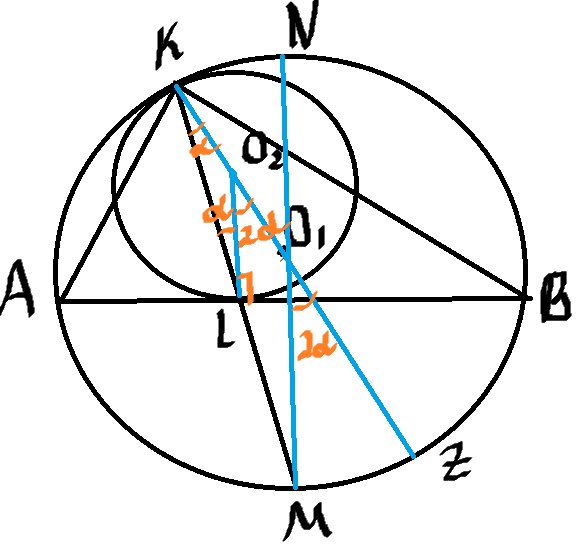
Итак, для чего мы это сделали? А вот зачем.
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. (1)
То есть, если мы докажем, что AB⊥NM, то дуги AM и MB будут равны, а значит и углы которые опираются на них будут равны! То что нам нужно!
Заметим, что треугольник \( KO_{2}L \) – равнобедренный (так как \( KO_{2}=O_{2}L \) – как радиусы
Пусть \( ∡LKO_{2}=∡O_{2}LK=α \)
Значит угол \( ∡LO_{2}O_{1}=2α \) (внешний угол треугольника равен сумме двух других углов не смежных с ним)
\( ∡FKM=\frac{1}{2}∪MZ \) значит \( ∪MZ=2α \)
\( ∡MO_{1}Z=2α \) (центральный угол)
Получаем, что \( ∡LO_{2}Z=∡MO_{1}Z \) (а эти два угла соответственные)
Значит прямые \( LO_{2}∥O_{1}M \) , но у нас же \( LO_{2}⊥AB \) (по свойству касательной), значит и \( MN⊥AB \)
Отлично, теперь применяем свойство которое я писал ранее. (1)
\( ∪AM=∪MB \) значит и \( ∡AKL=∡LKB \) . Делаем вывод, что KL – биссектриса.
б) Сделаем новый рисунок
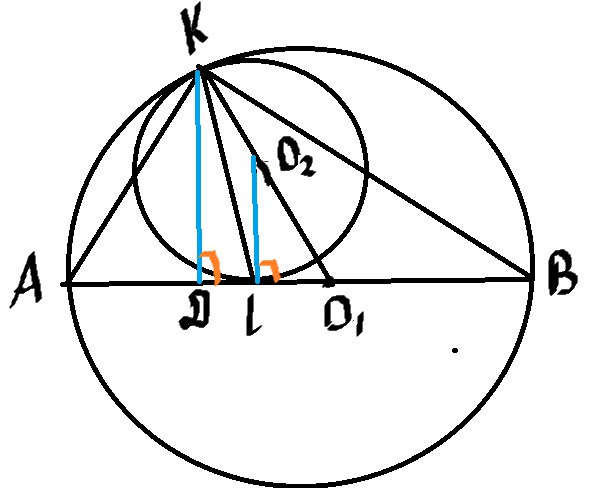
Угол \( ∡AKB=90° \) – очень важное условие. Значит AB-диаметр, и центр большей окружности O1 лежит на середине AB.
Опустим высоты KD на AB
Нам дано, что \( KO_{1}=6 \), \( KO_{2}=2 \)
\( O_{2}O_{1}=KO_{1}-O_{2}K=6-2=4 \)
Рассмотрим треугольник \( LO_{2}O_{1} \)
\( LO_{1}=\sqrt{4^2-2^2}=\sqrt{12}=2\sqrt{3} \)
\( ▲KDO_{1} \) подобен \( ▲LO_{1}O_{2} \) (по двум углам)
\( \frac{KD}{O_{2}L}=\frac{KO_{1}}{O_{1}O_{2}}=1.5 \)
Значит \( KD=1.5*O_{2}L=3 \)
\( DO_{1}=1.5LO_{1}=3\sqrt{3} \)
\( DL=DO_{1}-LO_{1}=3\sqrt{3}-2\sqrt{3}=\sqrt{3} \)
\( KL=\sqrt{KD^2+DL^2}=\sqrt{3^2+3}=\sqrt{12}=2\sqrt{3} \)
