- 16. В треугольнике ABC на AB, как на диаметре, построенаокружность ω1, а на AC, как на диаметре, построена окружность ω2. Окружности ω1 и ω2 пересекаются в точке М, отличной от точек А, В и С.
- А) Докажите, что точки М, В и С лежат на одной прямой.
- Б) Пусть АМ = 6, а диаметр окружности, описанной около треугольника АВС, равен 10. Найдите произведение АВ*АС.
16. В треугольнике ABC на AB, как на диаметре, построенаокружность ω1, а на AC, как на диаметре, построена окружность ω2. Окружности ω1 и ω2 пересекаются в точке М, отличной от точек А, В и С.
А) Докажите, что точки М, В и С лежат на одной прямой.
Б) Пусть АМ = 6, а диаметр окружности, описанной около треугольника АВС, равен 10. Найдите произведение АВ*АС.
Решение
Изобразим рисунок (чтобы увеличить кликните по фотографии)
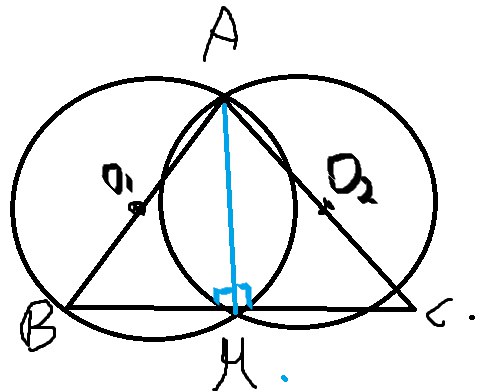
O1-центр первой окружности
O2-центр второй окружности
M-точка их пересечения.
Пункт А
Заметим, что \( ∡BMA=90° \) (так как этот угол вписанный и опирается на диаметр AB)
Заметим, что \( ∡CMA=90° \) (так как этот угол вписанный и опирается на диаметр AC)
Получаем что \( ∡BMC=180° \) (он развернутый, значит, что точки B M C лежат на одной прямой, что и требовалось доказать)
Пункт Б
\( S_{ABC}=\frac{abc}{4R} \) – abc – стороны треугольника
Диаметр мы знаем 10, значит радиус \( R=0.5D=5 \)
\( S_{ABC}=\frac{AB*AC*BC}{4R} \)
\( S_{ABC}=0.5*AM*BC \) – так как AM-высота
Приравняем две площади и выразим это произведение
\( 0.5*AM*BC=\frac{AB*AC*BC}{4R} \) – сократим на BC
\( 0.5*6=\frac{AB*AC}{4*5} \)
\( AB*AC=60 \)
Ответ: 60
