16. Точка О -центр окружности, описанной около остроугольного треугольника АВС.
На луче АО отмечена точка М так, что BAC + AMC= 90.
а) Докажите, что существует точка Р, одинаково удаленная от точек В, О, С, М.
б) Найдите расстояние от точки Р до точки М, если известно, что BAC 15 и
ВС=15.
Пункт А) Сделаем рисунок, пусть угол \( ∠BAC=α \), тогда угол \( ∠AMC=90-α \)
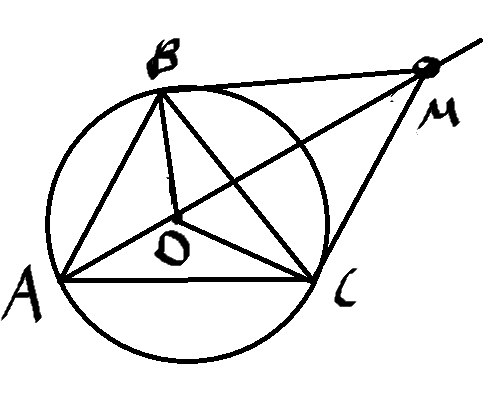
O-центр описанной окружности
Тогда угол \( ∠BOC=2α \) (т.к он центральный, а угол \( α \) вписанный)
Треугольник \( BOC \) – равнобедренный, \( BO=OC \) – как радиусы окружности.
Найдем углы \( ∠OBC=∠OCB=\frac{180-2α}{2}=90-α \)
Получаем два угла \( ∠OMC=∠OBC=90-α \) которые опираются на одну и туже прямую, значит около четырехугольника \( BOCM \) можно описать окружность.
А точка P-центр описанной окружности и она равноудалена от всех точек четырехугольника.
Пункт Б)
Если угол \( ∠BAC=15 \) то угол \( ∠BOC=30 \)
Получается, что угол \( ∠BOC \) – вписанный
Рассмотрим треугольник \( BOC \)
По обобщенной теореме синусов
\( 2R=\frac{BC}{sin∠BOC} \) получаем \( R=\frac{BC}{2sin30}=\frac{2*15}{2}=15 \)
Ответ: 15
